Counting Depth First Search Run-times
by Paul Marchertas
Here I discuss the combinatorics of the depth first search algorithm (DFS) on Hamiltonian graphs. As we are limited to Hamiltonian graphs, we start by generating them. Following standard notation, the size of a graph is m and the order of a graph is n. I will use Hn,m for the Hamiltonian graphs of a given order and size, while I will use n,m for the unlabeled Hamiltonian graphs since they are equivalence classes of labeled graphs. The simplest H are cyclic graphs (Cn = Hn,n). Another important class of H are complete graphs (Kn = Hn,Tn). For a given order of graph, the size of the H ranges from the cyclic graphs to the complete graphs.
∀G∊Hn, size(Cn) = n ≤ m ≤ size(Kn) = Tn
The smallest H is the three cycle, C3 = K3. H of order 4 have sizes 4, 5, and 6. Order 5 H5 have a maximum size of 10. The size of a complete graph (for a given order) is the nth triangular number.
Tn = ½((n – 1)2 + (n – 1))
figure 1. Here is a depiction of 3, 4, and 5.
A naive way to enumerate graphs is to start with a polygon (as a cycle) and choose the edges inside. This will not work (by itself) because the cyclic subgraph that we start with is unlabeled, while the generated subgraph is labeled. To enumerate the , we can add edges to cyclic graphs or remove edges from complete graphs, but we must eliminate redundancy. For convenience, I will refer to graphs generated in this manner by the number of edges added to a cyclic graph (exa. 5,7 ∊ +2 = m - n). From these pictures we can see that the graphs must be invariant under rotation and reflection. The symmetries of a circuit are indead a dihedral group (Dn, more on that latter).
figure 2. Here are some cyclic plus one edge graphs.
The number of unlabeled cyclic plus one edge graphs (in other words |n,n+1|) increases by one at every other increase in the order of . We can see that the added edge induces two cycles, that we can use to characterize the graph. For example, Cn plus one three cycle results in a unique unlabeled graph. When adding more than one edge, the added edges (or cross edges, cross links) themselves can still be described by the cycle they induce assuming that the edge is considered with respect to the original cyclic graph (i.e. the Hamiltonian circuit must be fixed). With more than one cross edge, the orientation of edges is also needed to uniquely identify an , so that unlabeled graph is not identified by the kind of cross edges alone.
figure 3. Here are some cyclic plus two edge graphs with two Hamiltonian circuits.
Plus two edges is a special case for multi circuit graphs; each n,n+1 of plus one will have an associated plus two n,n+2 with two Hamiltonian circuits. When a second circuit is formed by a pair of cross links, those edges must have the same length in our pictures. That is because those edges induce the same size cycles. Based on their appearance in these diagrams, I call them bow ties. The general case for multi circuit graphs is less convenient. For H with few edges (m < 2n) a second circuit must share segments with the first circuit. The last picture in figure 1 has a circuit that does not share any edges with the original circuit (the star).
1 order -->
1
1 1
1 1 1
2 2 1
2 6 2 1
1 12 10 3 1
1 16 32 19 3 1
s 16 82 87 27 4 1
i 12 158 339 182 42 4 1
z 6 232 1032 1026 365 56 5 1
e 2 266 2526 4590 2738 644 79 5 1
1 232 4992 16658 16530 6326 1109 100 6 1
| 158 8063 49698
v 82 10718 123915
32 11778
10 10718
2 8063
1 4992
2526
1032
339
87
19
3
1
table 1. Here is a table of |n,m|.
The graphs of the first three columns of the table are depicted in figure 1. The most edges a graph can have are the number of vertices squared. The number of possible cross edges (n2 - n). For n,m removing edges from complete graphs really is the same as adding edges to cyclic graphs. The process of choosing an edge to add (or remove) is made from the edges that have not been chosen. That is a hypergeometric distribution. The distribution of n,m shown in the table is related to the hypergeometric distribution in an analogous way to how Pascal’s triangle is related to the binomial distribution.
For every unlabeled graph there may be many labeled graphs, but the number is reduced by redundancy. The redundant labeled graphs correspond to groups via group action. Often, we need to deal with more than one unlabeled graph at a time so we can use Pólya enumeration theorem or in simpler cases Burnside's lemma. I'll point out a few simple cases. Complete graphs have full symmetry, so they only have a single labeled graph (|Kn| = 1). Cyclic graphs are same under reflection and rotation, so there number is reduced by half and divided by the order ( |Cn| = ½(n – 1)! ). The unlabeled plus one n,n+1 increase for even graphs, but the new cross edge (the highest minimum induced cycle edge) goes through the center and repeats half way around, so that half of its graphs are redundant. Every time there are redundant labelings due to rotational symmetry, the repetition divides the order. Prime ordered graphs cannot have 'extra' redundancy and are limited to circuits. There won't be a simple formula for |n,m|, but the prime number theorem might be enough for a bound.
1 order -->
3
6 12
1 60 60
90 540 360
45 1890 5040 2520
10 3070 30240 50400 20160
1 2607 96390 453600 544320 181440
s 1335 179550 2343600
i 455 214200 7546560
z 105 178500 -
e 15 111030 -
1 53592 -
| 20307 -
v 5985 -
1330 -
210 -
21 -
1 -
-
-
-
-
-
-
1
table 2. Here is a table of |Hn,m|.
The symmetries of Hamiltonian circuits relate to dihedral groups. To get the group for a multi circuit graph we can use group generators. While we cannot union groups together to form another group, group generators can be unioned to form the generator of a group. As more generators are combined, they will induce the cycles of other circuits. The circuits clump together as edges are filled in. (How does that work? How does this process generalize prime numbers? Should we use n,m,c notation?) In Kn, ½(n – 1)! circuits have to fit inside. Here are a few counts of Hamiltonian circuits of unlabeled graphs.
Multi circuit graphs will have more redundancy and so fewer labeled graphs. Notice that the distribution of n (in table 1) is symmetric over m and the distribution of Hn (in table 2) is asymmetric. Unlabeled structures tend to be generated by exponential generating functions. As enumerating Hamiltonian graphs interleaves labeled and unlabeled graphs, it may be that n or Hn are generated by a ratio of exponential generating functions, aka a hypergeometric function. Burnside ring may be useful too.
I acknowledge my limited understanding and explanation of the combinatorics of Hamiltonian graphs, but I have not found another.
The time that DFS takes to compute its output has to do with complexity. Complexity is based on string length. I won’t go into detail why complexity theory requires this. What we need to know is that string length effects the order of enumeration. While string length is traditionally used to account for information content, we use graphs as an abstract data type. In place of string length we use graph size times the logarithm of the order (m log(n) ). Thereby, size is more significant than order. While we have added edges to Hn,n+e as a conceptual explanation, this is contrary to the direction string length indicates. The conventional enumeration of graphs moves top to bottom down a column then left to right on table 1, but the information ordered enumeration goes left to right across rows then top to bottom on table 2. In other words, Hn,m is enumerated by size range, starting from graphs of the minimum order (for their size) to cyclic graphs (by removing edges) before going to larger sized graphs.
size 3 4 5 5 6 6 6 7 7 7 8 8 8 8 9 9 9 order 3 4 4 5 4 5 6 5 6 7 5 6 7 8 5 6 7 #H 1 3 6 12 1 60 60 90 540 360 45 1890 5040 2520 10 3070 30240 size 9 9 10 10 10 10 10 10 11 11 order 8 9 5 6 7 8 9 10 6 7 #H 50400 20160 1 2607 96390 453600 544320 181440 1335 1795500
table 3. A table of number of Hn,m in order of enumeration.
So now that we have some graphs, we can search them. To measure the time used by a search algorithm, we can measure the growth of the search tree. The depth first search algorithm (DFS) searches for a path by changing one edge at a time, so the search tree is a walk through the graph. (Note, I have neglected to include to count backtracking. This needs to be accounted for because instruction sets / the model of computation should have constant time operations. The use of finite state machines / regular grammars here is acceptable because we will be focused on differences greater than polynomial factors. Even though it won’t end up making a difference you can convert the timings by doubling them and subtracting n. ) For the depth first search algorithm, the current path will backtrack if and only if it is not contained within a Hamiltonian circuit. Therefore, the branches / choices that matter (for the use of time) are the ones that have non circuit edges (and circuit edges, while the path is in circuit). After the search path leaves a circuit, it will have to backtrack, but before backtracking it will span the remainder of the graph. The part of the search walk that searches the remainder of the graph forms a covering walk. The remaining graph may have cycles, so, in general, the amount of time that DFS takes to walk it may be affected by the labeling of the graph. Which branches are taken first do not always affect the size of the covering tree (and so do not affect time). The amount of the circuit covered before leaving the circuit (with adjacent edges) affects the amount of graph remaining to be covered and, thereby, the time needed by DFS. The start vertex and direction can affect the size of the walk, without changing the size of the remaining graph. We will need to understand which branches influence the size of the walk to predict DFS timings. ‘What is known and when is it known’ is a common theme of NP-complete problems. Early choices limit later choices. (hypergeometric again)
figure 4. Here are all 6,7 search configurations preceding a branch.
Plus one Hn,n+1 only have one opportunity to diverge from the circuit. If the path stays on the circuit, then it goes around the circuit as if the graph was cyclic. The minimum time to recognize the graph as Hamiltonion is the path around the circuit ( DFStime(g) ≥ n ). The number of labeled plus one graphs of DFS time equal to the order (i.e. minimal time) will be more than half (of all |Hn,n+1| ). They are more than half because sometimes the cross edge will intersect the start vertex. At the start vertex the direction that the path will take around the circuit is not yet fixed, so there are three branches rather than two. The next greater time (for all Hn,n+1) is two greater than the order (timeDFS(Hn,n+1) ≤ n + 2). No Hn have an order plus one time because the minimum cross link is a three cycle, so one edge must be taken (and repeated) in addition to the cross link. There is also the possibility of a second orientation with respect to the initial path. Here (in figure 4) there is only one, the three cycle in the back direction (not counting the start vertex). Notice that the four cycle is limited to being rotated one less edge away from the start vertex. Since the four cycle goes thru the center (the cross link induces two four cycles), it has only one orientation. This holds in general; The shorter the cross edge the fewer rotations are backward and more are forward. The start vertex has a full complement of unlabeled graphs (with orientations). The number of Hn,n+1 of one cross-link where the link intersects the start vertex seem to be: OEIS: A181967. I guess it could make sense: normalizers vs fixed point, alternating groups vs a choice of two directions (cyclic orders), adding by one to the graph vs multiplying prime cycles.
4 5 6 7 8 9 DFS time -->
1 1
38 4 10 8
330 20 50 80 60
3000 120 300 480 660 480
29400 840 2100 3360 4620 5880 4200
312480 6720 16800 26880 36960 47040 57120 40320
table 4. A table of |Hn,n+1| for a given DFS time (see dfs_times.csv for more)
There are two more things we need to produce a formula for the number of plus one Hn,n+1 for a given search time. The range of the DFS timings for plus one edge Hn,n+1 is from the order to one less than twice the order (n ≤ DFStime(Hn,n+1) ≤ 2 – 1). The other thing to know is that last vertex, before the start vertex, is constrained as being greater than the vertex on the other side of the start vertex. The order plus two time (for H6,7) has two thirds the number of (i.e. labeled graphs for each unlabeled graph) as most times. The longest time (i.e. slowest run-time) is for cross edges at the start vertex which is another special case. The fastest times are a special case as well.
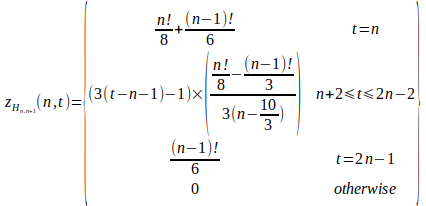
The formula for the number of Hn,n+1 for a given order and DFS time.
Plus one is a simple case, but the formula that we get is reasonably complicated. This formula is not useful, but it describes a bit of the pattern we are looking at. We have not even needed to account for multiple Hamiltonian circuits! It may be possible to discover a general formula (where the size is a parameter, rather than being fixed to the order). I don’t actually need an explicit formula for my purposes.
Search walks form a hierarchy / tree from back to front. All accepting search walks end the same way, with the last edge of the path. There become more than one ending further back from the end; there can be a branch for a three cycle. The combinatorial possibilities grow the further we go from the end. Each search walk ending will be reused an infinite number of times, so it won't help to count the branches. The rate that branches are reused might be useful to set a bound on the distribution of timings.
There is a lot I could say comparing graph theory with topology. I will point out that walks are topologically continuous. It is something that we take for granted, but I have found a topological perspective instructive for graph theory. Another thing that goes overlooked is that the depth first search algorithm must start by checking for a global property (is this the circuit). While this check seems unremarkable for analgorithm, it makes a difference that complicates the combinatorics. Running the algorithm on a subgraph does not get the same result beacuse the global property should not be reset. Imagine if we use an algorithm that does not have that check. We could call it depth first exploration. We might wonder if depth first search would be better named depth second search. That would be too annoying now that we are used to DFS, so I talk about search walks and covering walks instead. Notice that every accepting search walk is a truncation of a covering walk and every non-trivial (non cycle) search walk has a covering walk (of a sub graph) inside it.
The following is my former attempt to explain my work. I don’t think it was good because it continues from the previous discussion. It is sort of backwards. As I’m not going to try to fix it up now, so I can’t recommend it. Try ‘PNP here’ first.
When a search algorithm is applied over a combinatorial class, it should be possible to define a recurrence relation. The search tree for DFS is a walk on / in a graph. The walk will induce a subgraph. If the induced subgraph is smaller than the graph (, but always the same order), then some edges are not covered / used (are blocked from the point of view of the search). When edges are blocked (for DFS of a labeled H), then the walk on a graph repeats one of the walks (and thereby labelings) on the induced (unlabeled) subgraph. Only cyclic graphs do not have a walk that is a recurrence of an earlier graph. Cyclic graphs are guaranteed to have minimum time already. Many labelings will block an edge, but only graphs without non-circuit (cross) edges will have a recurrence for every labeling (such as those in figure 3). For every branch where one set of circuits is selected and another set of circuits is deselected an edge is blocked (if it has not been covered already via a non-circuit cross edge). If a graph and labeling result in a walk (i.e. DFS of a labeled graph) that covers all the edges, then that graph with that labeling is an initial occurrence. { Hamiltonian circuits can be represented by rotation groups. They can also be represented, more succinctly, by cyclic orders with their inverse cyclic orders (in effect, undirected cyclic orders). Multi circuit H have more ways to have recurrences, such that the rotational symmetries of a H form a hierarchy / tree. The initial occurrences (roots of the forest?) form a boundary. It should be possible to form a topological space over the collection of all permutation groups formed / generated by rotations. }
We have seen that this seemingly simple algorithm relates to algebra, topology, and number theory, but I have not yet mentioned analysis. My goal is to prove a lemma. I think it would be good to prove that there exists a polynomial bound on a polynomial fraction of the time resource function of DFS (of strings that the depth first search algorithm accepts). This seems a reasonable proposition, since there are always a substantial fraction of labeled H that have a DFS time equal to the order. Those minimal time, labeled H are not only within polynomial time, but within linear time. I only have a vague notion for a proof strategy: when recurrence happens with many (a large enough proportion of) labeled H (such as when the fraction of minimal timed recurrences is too few / too small a proportion to make up the polynomial fraction), the (time resource) distribution of graphs is within the (earlier / smaller) bound condition, so that leaves room for some initial occurrences to still be within the bound condition at the current position (particularly because the recurrences are more than one inductive / string length step back). There are many steps to a proof, but that is idea I am pursuing. { I don’t know if it has occurred to you that we are trying to analyze a decision problem that is not deciding any thing. Of course, it is not the decision problem we are analyzing, but the resource function (of a single algorithm). You may even be wondering if the symmetry in the domain may impact not only the resource function, but possible algorithms. Wait, wait! You are way ahead of me. }
With the lemma, ‘fast’ inputs are able to vouch for the ‘slow’ inputs. Let’s modify DFS to process a polynomial number of input strings in parallel up to a polynomial time limit. After reaching the time limit, if any string was accepted by DFS, then all the inputs (among those processed, up to the accepted input) are accepted. Now we have a high dimension version of DFS. Be sure to understand that this new algorithm takes different (sparser) input, so it has a different computable function. It is interesting that an algorithm and problem so similar to what we started with can be within a polynomial bound (using the original string length and assuming we can prove the lemma). All that is needed is to sort the input to space out the ‘fast’ inputs. Sorting the input (within string length boundaries) would take a long time, but that is outside the function and therefore not measured by the complexity bound. { It may seem that this is just a strange and elaborate way to reformulate the P =? NP problem. That is correct. Consider that we are already in a position to wonder that doing infinitely more work (at the limit) is faster. }
There are practical reasons why we don’t think to sort the domain, but this about the limitations of our theory rather than practicality. Since we have chosen a theory of complexity to be insensitive to the model of computation (and thereby the encoding of input), complexity has a different basis than computation. While we may like to think of the unrelatedness of inputs as being more general, we must remember that all computable functions are countable and can be ordered. Consider that we can modify our high dimension DFS to start with a single input. We can use an index function to return the position in the order of a value and an inverse index function to generate a value at a location. The choice of order is more difficult (for this function) because it will affect the speed we can obtain from our index and inverse index functions. This shows that the algorithm (up to isomorphism?) and its resource function (for a NP-complete problem) depends on the order of input. As it depends on the order of the input it also depends on the encoding used. The P =? NP problem is therefore logically independent (assuming we can prove the lemma). { No doubt, you can think of objections. For example, DFS is only one algorithm. We can assume that if P = NP then any NP-complete algorithm is convertible to another in polynomial time (by choice of a model of computation). I believe that, for non trivial cases, independence does not have the decisive arguments that we want because of incompleteness. }
{ I was not going to mention this alternative; just to simplify things. Since I’m not done and don’t expect that to change soon, so I can’t summarize or avoid exploring unnecessary topics. I focused my argument on P = NP because I thought it would be hard to argue with combinatorics. } If you prefer an argument based on P ≠ NP, then put the ‘extra’ structure / order / information inside the complexity class. Since P is known for search and sort algorithms, we use the notion of walking on a graph as an alternative definition of P. Graph problems are about walking or partitioning; in other words about continuity or discontinuity. I think it is helpful to map graphs to topological spaces.
![]()
{ My set theory is rusty, so I need to check these formulas! } We can use a graph location topology (based on adjacency) or graph connection topology. { These topological spaces are more in keeping with keeping with graph theory than using a simplicial complex to form a hull. Note that labeled graphs induce an order on the object set in the topological space. Labeled directed graphs result in doubly ordered (object set and topology set) topological spaces. I don’t know of anyone else to have proposed formalizing functions as doubly ordered topological spaces. } Now, our requirement of PTIME algorithms being consistent with walks on graphs has a more familiar formalism, open-set continuity. We need to add a requirement that is difficult to formalize without using topology. The requirement is that P is Euclidean (or some such global / topological property). Then you can go about proving that NP is a (non-homeomorphic) manifold of P, if you prefer that alternative over my lemma. Again P =? NP supposes infinite properties (trans-generative properties) that cannot be determined from the axioms.